Для каждой предложенной модели необходимо получить в Calc численные данные изменения популяции, построить графики изменения популяции, посмотреть на изменения картины в зависимости от начальных размеров популяции и параметров модели, сделать выводы.
1. Модель неограниченного роста
Пусть популяция состоит только из одного вида. Моделирование численности популяции будем производить по периодам, например, месяцам или годам.В первой, самой простейшей модели, популяция не имеет никаких ограничений по росту. Обозначим размер популяции в период \(N\) через \(x_N\). Выразим размер популяции в следующий период времени \(x_{N+1}\) через \(x_N\). В модели неограниченного роста прирост популяции пропорционален размеру самой популяции, поэтому \(x_{N+1}=ax_N\), где \(a\) – некоторый коэффициент. Например, если ежегодный прирост популяции составляет \(2\%\), то \(a=1{,}02\). Значение \(a>1\) соответствует росту популяции, значение \(a<1\) – убыванию популяции.
Полученные рекуррентные соотношения вычислим в электронной таблице. Заполним столбец A номерами периодов от 1 до 200, в ячейке A1 запишем название столбца "Период". В ячейке B1 напишем название столбца "Популяция", в ячейке B2 – начальное значение популяции – 1000, в ячейке D1 запишем значение коэффициента \(a\) равное \(1{,}02\). В ячейку B3 запишем рекуррентную формулу вычисления численности популяции в следующий период: B3=B2*$D$1. Затем содержимое этой ячейки скопируем в ячейки B4:B201.
Мы получили значения популяции в каждый период. Теперь построим график значения популяции в периоды времени. Для этого выделим блок A1:B201, выберем в меню "Вставка – диаграмма", выберем тип диаграммы – "Линии – Только линии", на шаге "2. Диапазон данных" необходимо отметить пункты "Первая строка как подпись", "Первый столбец как подпись".
Полученный график называется графиком показательной функции (или экспоненциальной) и демонстрирует быстрый рост популяции в условиях неограниченной возможности для роста.
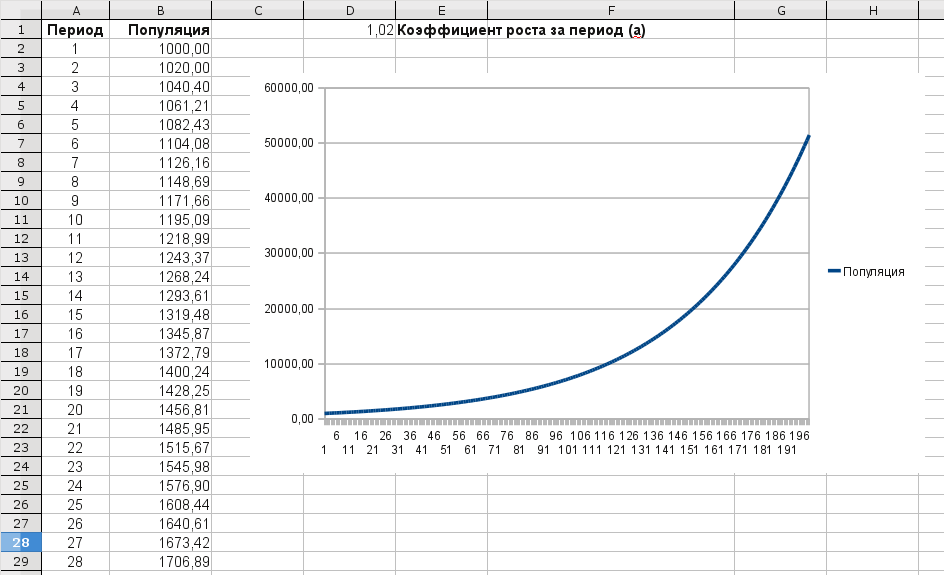
Постройте данную модель для значения параметров \(x_1=1000\), \(a=1{,}02\).
Измените значение параметра \(a=1{,}01\), \(a=1{,}03\), \(a=1\), \(a=0{,}99\), \(a=0{,}98\). Объясните полученные результаты.
2. Модель ограниченного роста
На самом деле возможности неограниченного роста у популяции нет, так как обычно возможности роста ограничены. Например, популяция волков в лесу ограничена, поскольку каждому волку для прокорма необходима некоторая территория, на которой не может прокормиться неограниченное число волков. Если ареалы обитания отдельных волков пересекаются, то объем пищи, который достается каждому из них уменьшается и уменьшается скорость роста популяции.Введем в формулу дополнительный член, замедляющий скорость роста в случае большой популяции. Будем считать, что это замедление зависит от вероятности встречи двух волков. Поэтому этот дополнительный член будет зависеть от вероятности встречи двух волков, который, в свою очередь, растет, как квадрат количества волков.
Получаем формулу рекуррентного соотношения для модели ограниченного роста:
\[x_{N+1}=ax_N-bx_N^2.\]
Здесь значение коэффициента \(b\) должно быть существенно меньше коэффициента \(a\).
Постройте данную модель для значения параметров \(x_1=1000\), \(a=1{,}03\), \(b=10^{-5}\).
Подберите значения начальной популяции и параметров так, чтобы величина популяции убывала.
Как определить предельное значение, к которому стремится популяция?
3. Модель ограниченного роста с отловом
Эта модель отличается от предыдущей наличием дополнительного отлова \(c\) особей каждый период, поэтому рекуррентное соотношение имеет следующий вид.\[x_{N+1}=ax_N-bx_N^2-c.\]
Постройте модель ограниченного роста с отловом для значения параметров \(x_1=1000\), \(a=1{,}03\), \(b=10^{-5}\), \(c=10\).
4. Модель хищник-жертва
В модели хищник-жертва имеется две популяции – жертвы и хищники, например, зайцев и волков. Обозначим популяцию жертв в период \(N\) через \(x_N\), популяцию хищников через \(y_N\). Прежде всего начнем с соотношений, не учитывающих межвидовое взаимодействие на основе формул ограниченного роста:
\[\cases{x_{N+1}=a_1x_N-b_1x_N^2,\cr y_{N+1}=a_2y_N-b_2y_N^2.}\]
Теперь добавим межвидовое взаимодействие. Вероятность встречи жертвы и хищника пропорциональна произведению их количества \(x_Ny_N\). Добавим соответствующие слагаемые в формулу:
\[\cases{x_{N+1}=a_1x_N-b_1x_N^2+c_1x_Ny_N,\cr y_{N+1}=a_2y_N-b_2y_N^2+c_2x_Ny_N.}\]
Для жертвы встреча с хищником сказывается негативно на росте популяции, поэтому \(c_1<0\). Для хищника, наоборот, встреча с жертвой – это получение пищи, что положительно влияет на рост популяции, поэтому \(c_2>0\). Осталось только заметить, что для жертв \(a_1>1\), поскольку в отсутствии встречи с хищником популяция жертв будет расти, а вот для хищников \(a_2<1\), так как без жертв хищники будут вымирать ввиду отсутствия пищи.
Постройте модель хищник-жертва для следующих параметров: \(x_1=1000\), \(a_1=1{,}05\), \(b_1=2\cdot10^{-6}\), \(c_1=-10^{-4}\), \(y_1=500\), \(a_2=0{,}95\), \(b_2=2\cdot10^{-6}\), \(c_2=10^{-4}\).
По данным моделирования постройте диаграмму типа X-Y – это диаграмма, на которой по оси OX откладывается число жертв, по оси OY – число хищников, если в момент времени \(N\) имеется \(x_N\) жертв и \(y_N\) хищников, то это соответствует точке \( (x_N, y_N) \) на диаграмме.
Увеличьте начальное число жертв, рассмотрите случаи \(x_1=2000\), \(x_1=3000\), \(x_1=4000\), \(x_1=5000\). Поясните полученные результаты.
Сравните свои наблюдения с данными о заготовке пушнины в Северной Америке, добытых Компанией Гудзонова залива:
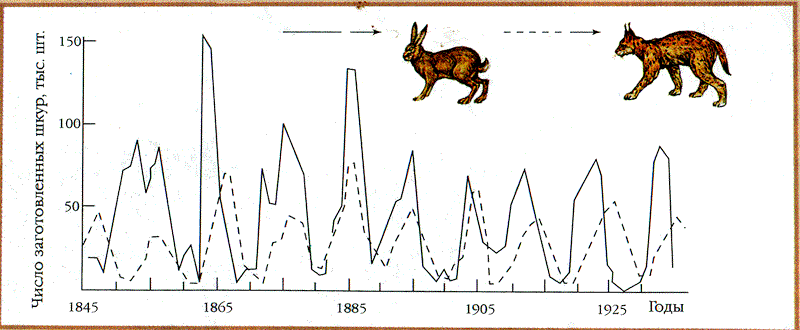
5. Конкурентная модель
В конкурентной модели – два вида, которые не нуждаются друг в друге, но при этом конкурируют за общие ресурсы. Каждый вид может расти без другого вида, но при этом столкновение двух видов вредит им обоим. Рекуррентные соотношения в этом случае такие же, как в предыдущей задаче, только \(a_1>1\), \(a_2>1\), \(c_1<0\), \(c_2<0\).Постройте конкурентную модель для следующих параметров: \(x_1=500\), \(a_1=1{,}03\), \(b_1=5\cdot10^{-5}\), \(c_1=-10^{-4}\), \(y_1=500\), \(a_2=1{,}01\), \(b_2=10^{-5}\), \(c_2=-10^{-4}\).
Поменяйте начальные размеры популяций и параметры популяций. Возможна ли ситуация сосуществования двух конкурентных видов, когда размер их популяции остается стабильным?
6. Симбиотическая модель
Организмы-симбиоты нуждаются друг в друге для существования, ни один из них не может существовать без другого.В данной модели \(c_1>0\), \(c_2>0\), \(b_1>c_1\), \(b_2>c_2\) (эти неравенства нужны чтобы избежать ситуации бесконечного роста популяций).
Постройте симбиотическую модель для следующих параметров: \(x_1=1000\), \(a_1=1{,}06\), \(b_1=5\cdot10^{-4}\), \(c_1=10^{-5}\), \(y_1=1000\), \(a_2=1{,}03\), \(b_2=10^{-5}\), \(c_2=10^{-6}\).
Поменяйте начальные размеры популяций и параметры популяций.
7. Эпидемия
В городе проживает \(10^6\) человек, один из которых заболевает инфекционной болезнью. Продолжительность болезни – 7 дней, через 7 дней человек выздоравливает и перестает быть заразным для окружающих. Выздоровевший человек повторно не заболевает.
Количество новых заболевших в течение дня пропорционально числу встреч больных и здоровых, то есть равно \(k\times \text{число восприимчивых} \times \text{число больных} \), где число восприимчивых – это количество жителей, не заболевших до этого, число больных – количество заболевших в течение 7 последних дней. Значение коэффициента \(k\) положим равным \(3\times 10^{-7}\).
Постройте модель развития эпидемии. Постройте графики числа заболевших в течение дня, числа восприимчивых и переболевших людей.
Ответьте на вопросы:
1. Сколько дней будет продолжаться эпидемия?
2. На какой день будет пик развития эпидемии?
3. Какое число людей заболеет в день пика развития эпидемии?
4. Сколько людей переболеет в итоге?
Форматтер highlight/comments отсутствует