Задание Tree-1

Напишите рекурсивный алгоритм алг Тонкое дерево (арг вещ длина, арг цел глубина), где
длина – длина ствола дерево, глубина – количество развилок на ветках.
На каждой развилке ветка разветвляется на две ветки, каждая из которых в \(\sqrt2\) раз короче исходной ветки.

Ниже приведены результаты вызова этого алгоритма для разного набора параметров:

Тонкое дерево (110, 0)

Тонкое дерево (110, 1)

Тонкое дерево (110, 2)

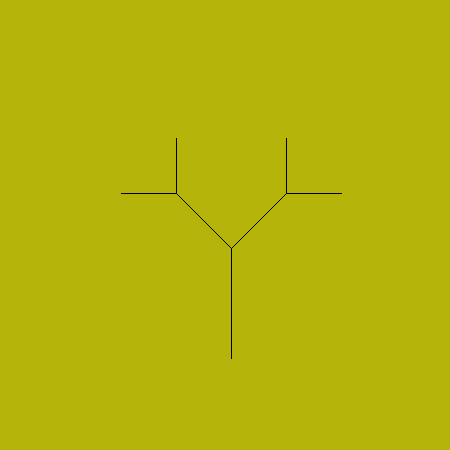
Тонкое дерево (110, 3)

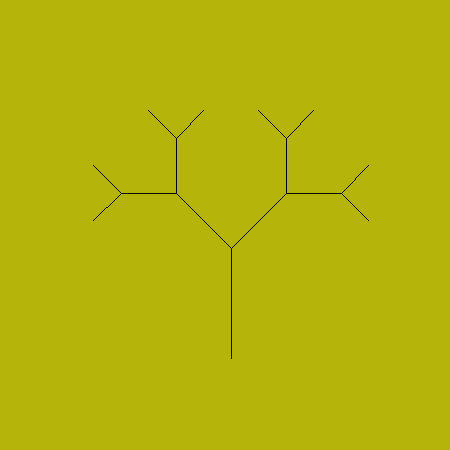
Тонкое дерево (110, 4)

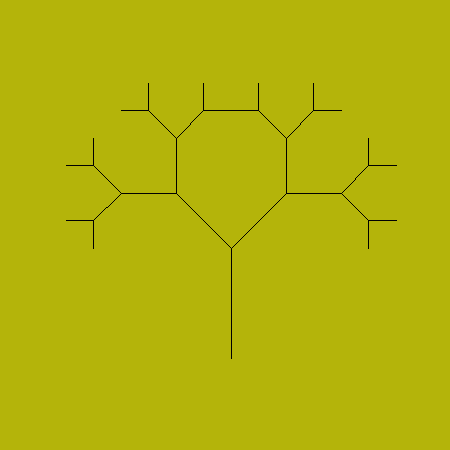
Тонкое дерево (110, 7)

Тонкое дерево (110, 10)

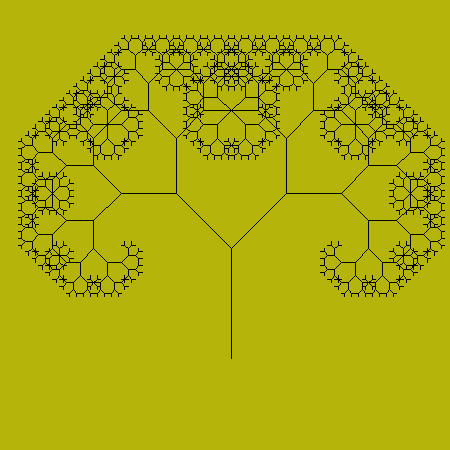
Задание Tree-2

Модифицируйте функцию алг Тонкое дерево (арг вещ длина, арг цел глубина) так, чтобы ей можно было передавать в качестве параметра углы, под которыми разветвляется дерево.

Пример дерева с измененными углами:

Задание Tree-3

Модифицируйте функцию алг Тонкое дерево (арг вещ длина, арг цел глубина) так, чтобы ей можно было передавать в качестве параметра углы, под которыми разветвляется дерево а также коэффициенты, задающие длины веток после ветвления.

Пример дерева с измененными углами и разными длинами веток:

Задание Tree-4

Дерево на предыдущем рисунке обладает тем недостатком, что при фиксированной глубине рекурсии более длинные ветки дерева прорисовываются плохо, т.к. не заканчиваются короткими "листьями". Короткие ветки прорисованы хорошо и заканчиваются короткими "листьями", но при большой глубине рекурсии короткие ветки прорисовываются неоправданно долго, т.к. рекурсивно отрисовываются очень мелкие невидимые детали.
Модифицируйте алгоритм рисования дерева так, чтобы рекурсия останавливалась не по достижении фиксированной глубины, а когда размер отрисовываемых деталей станет маленьким. Это позволить делать более глубокую рекурсию для "длинных" веток, и более короткую – для "коротких".

Изображения, полученные таким образом, будем называть "пушистыми". Пример "пушистого" дерева:

Задание Tree-5

Нарисуйте лес, содержащий не менее 6 деревьев разного вида.