7Б 27.04.2009 Электронные таблицы
Все задания сдаются в
В некоторых заданиях есть еще дополнительные вопросы, ответы на которые нужно прислать по электронной почте.
Задание 6 (28.23*)
Вычислите 12+22+...+992.Ячейку с ответом выделите жирным шрифтом.
Задание 7
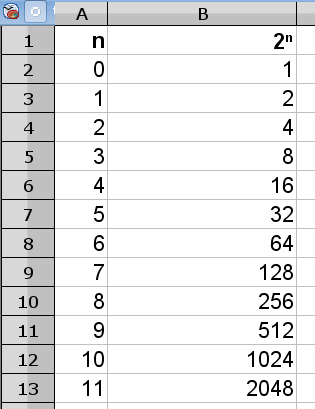
Постройте последовательность значений 2n для n от 0 до 60. Полученную таблицу сдайте в систему.Попробуйте ответить на вопросы:
- Почему значения 2n для n≥50 имеют такой странный вид и что означает этот вид?
- Какую максимальную степень двойки можно записать в ячейку электронной таблицы и чему примерно равна эта степень двойки?
Ответы присылать по электронной почте!
Задание 8
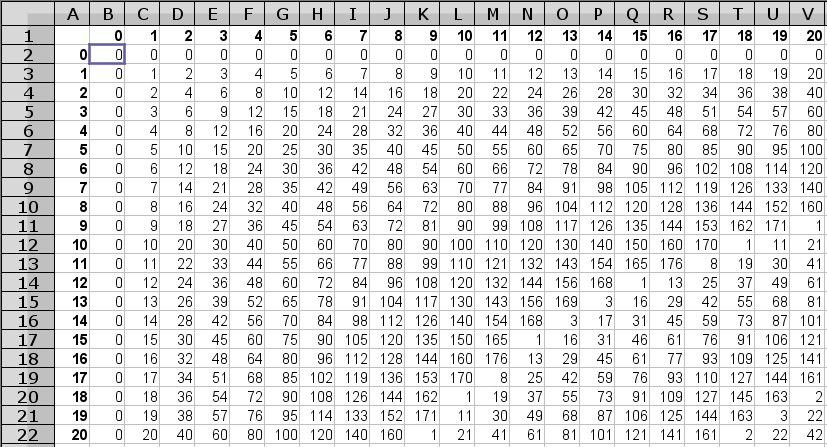
Постройте таблицу умножения остатков от деления на 179. В Вашей таблице должны быть указаны все возможные остатки от 0 до 178.Для вычисления остатка от деления величины A на величину B используется функция MOD(A;B).
Задание 9
Постройте таблицу значений остатков от деления 2n на 179. Пользуясь этой таблицей докажите, что величина 2n может давать все возможные ненулевые остатки при делении на 179. Доказательство присылать по электронной почте (а таблицу сдайте на проверку).
Задание 10 (28.10)
Докажите, что 13+23+...+20073 делится и на 2007, и на 2008.Задание 11 (28.11)
Докажите, что 22005+32005 делится на 11 и на 25, но не делится на 7.Задание 12 (28.12*)
Найдите 4 последние цифры числа 9999+5151.Задание 13
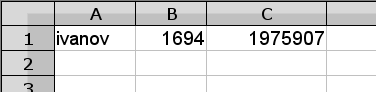
В ячейку A1 электронной таблицы запишите свой логин (строчными латинскими буквами).В ячейку B1 запишите формулу =1000+MOD(DECIMAL(SUBSTITUTE(A1;"_";;1);36);997)
В ячейку C1 запишите формулу: =10^6+MOD(DECIMAL(SUBSTITUTE(A1;"_";;1);36);999983)
Эти формулы нужно выделить на этой странице, скопировать и вставить в Calc. Не переписывайте формулы руками.
У вас получится какое-то четырехзначное число в ячейчке B1 и какое-то семизначное число в ячейке C1.
После этого вычислите остаток от деления 2B1 на C1. Ячейку, содержащую искомое значение, выделите жирным шрифтом и сдайте таблицу на проверку.
Задание 14
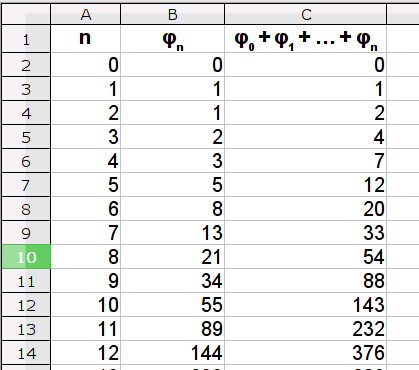
Последовательность Фибоначчи определяется следующим образом:φ0=0
φ1=1
...
φn=φn-1+φn-2
В следующей табличке выписаны первые члены последовательности Фибоначчи (столбец B):
Выполните задания:
- Вычислите все элементы последовательности Фибоначчи до φ60.
- Для каждого из n от 0 до 60 вычислите сумму начала ряда Фибоначчи φ0+φ1+...+φn. Проверьте, что φ0+φ1+...+φn=φn+2-1.
- Вычислите сумму квадратов начала ряда Фибоначчи: φ02+φ12+...+φn2. Проверьте, что φ02+φ12+...+φn2=φn×φn+1.
- Проверьте, что φn+3×φn – φn+2×φn+1=(-1)n+1.
- Проверьте, что φ2n=φn+12-φn-12.