Ранее была задача вычисления числа сочетаний из n элементов по k, для чего необходимо вычисление факториалов трех величин: n, k и n-k. Для этого можно сделать три цикла, что приводит к увеличению размера программы за счет трехкратного повторения похожего кода. Вместо этого лучше сделать одну функцию, вычисляющую факториал любого данного числа n и трижды использовать эту функцию в своей программе. Соответствующая функция может выглядеть так:
def factorial(n: int) -> int:
"""Return factorial of n."""
f = 1
for i in range(2, n + 1):
f *= i
return f
Этот текст должен идти в начале программы, вернее, до того места,
где мы захотим воспользоваться функцией factorial.
Первая строчка этого примера является описанием нашей функции.
factorial — идентификатор, то есть имя нашей функции.
После идентификатора в круглых скобках идет список параметров,
которые получает наша функция. Список состоит из перечисленных через запятую
идентификаторов параметров. В нашем случае список состоит из одной величины n.
В конце строки ставится двоеточие.
Далее идет тело функции, оформленное в виде блока, то есть с отступом.
Внутри функции вычисляется значение факториала числа n
и оно сохраняется в переменной f. Функция завершается инструкцией return f,
которая завершает работу функции и возвращает значение переменной f.
Инструкция return может встречаться в произвольном месте функции, ее исполнение
завершает работу функции и возвращает указанное значение в место вызова.
Если функция не возвращает значения, то инструкция return
используется без возвращаемого значения, также в функциях, не возвращающих значения,
инструкция return может отсутствовать.
Теперь мы можем использовать нашу функцию несколько раз.
В этом примере мы трижды вызываем функцию factorial для вычисления трех факториалов:
factorial(n), factorial(k), factorial(n-k).
n = int(input()) k = int(input()) print(factorial(n) // (factorial(k) * factorial(n - k)))
Мы также можем, например, объявить функцию binomial, которая принимает два целочисленных параметра
n и k и вычисляет число сочетаний из n по k:
def binomial(n: int, k: int) -> int:
"""Return binomial coefficient C_n^k."""
return factorial(n) // (factorial(k) * factorial(n - k))
Тогда в нашей основной программе мы можем вызвать функцию binomial
для нахождения числа сочетаний:
print(binomial(n, k))
Вернемся к задаче нахождения наибольшего из двух или трех чисел. Функцию нахождения максимума из двух чисел можно написать так:
def max(a: int, b: int) -> int:
"""Return maximum of a and b."""
if a > b:
return a
else:
return b
Теперь мы можем реализовать функцию max3, находящую максимум трех чисел:
def max3(a: int, b: int, c: int) -> int:
"""Return maximum of three intergers a, b, c."""
return max(max(a, b), c)
Функция max3 дважды вызывает функцию max для двух чисел:
сначала, чтобы найти максимум из a и b, потом чтобы найти максимум из этой
величины и c.
Внутри функции можно использовать переменные, объявленные вне этой функции
def f() -> None:
"""Print a to stdout."""
print(a)
a = 1
f()
Здесь переменной a присваивается значение 1, и функция f
печатает это значение, несмотря на то, что выше функции f эта переменная
не инициализируется. Но в момент вызова функции f переменной a
уже присвоено значение, поэтому функция f может вывести его на экран.
Такие переменные (объявленные вне функции, но доступные внутри функции) называются глобальными.
Но если инициализировать какую-то переменную внутри функции, использовать эту переменную вне функции не удастся. Например:
def f():
a = 1
f()
print(a)
Получим NameError: name 'a' is not defined. Такие переменные, объявленные внутри функции,
называются локальными. Эти переменные становятся недоступными после выхода из функции.
Интересным получится результат, если попробовать изменить значение глобальной переменной внутри функции:
def f():
a = 1
print(a)
a = 0
f()
print(a)
Будут выведены числа 1 и 0. То есть несмотря на то, что значение переменной a
изменилось внутри функции, то вне функции оно осталось прежним! Это сделано в целях
“защиты” глобальных переменных от случайного изменения из функции
(например, если функция будет вызвана из цикла по переменной i, а в этой функции
будет использована переменная i также для организации цикла, то эти переменные должны
быть различными). То есть если внутри функции модифицируется значение некоторой переменной,
то переменная с таким именем становится локальной переменной, и ее модификация не приведет
к изменению глобальной переменной с таким же именем.
Более формально: интерпретатор Питон считает переменную локальной, если внутри
нее есть хотя бы одна инструкция, модифицирующая значение переменной (это может быть
оператор =, += и т.д., или использование этой переменной
в качестве параметра цикла for, то эта переменная считается локальной
и не может быть использована до инициализации. При этом даже если инструкция,
модифицирующая переменную никогда не будет выполнена: интерпретатор это проверить
не может, и переменная все равно считается локальной. Пример:
def f():
print(a)
if False:
a = 0
a = 1
f()
Возникает ошибка: UnboundLocalError: local variable 'a' referenced before assignment.
А именно, в функции f идентификатор a становится локальной переменной,
т.к. в функции есть команда, модифицирующая переменную a, пусть даже никогда и
не выполняющийся (но интерпретатор не может это отследить). Поэтому вывод переменной a
приводит к обращению к неинициализированной локальной переменной.
Чтобы функция могла изменить значение глобальной переменной, необходимо объявить эту переменную
внутри функции, как глобальную, при помощи ключевого слова global:
def f():
global a
a = 1
print(a)
a = 0
f()
print(a)
В этом примере на экран будет выведено 1 1, так как переменная a объявлена, как глобальная,
и ее изменение внутри функции приводит к тому, что и вне функции переменная
будет доступна.
Тем не менее, лучше не изменять значения глобальных переменных внутри функции. Если функция должна поменять какую-то переменную, то как правило это лучше сделать, как значение, возвращаемое функцией.
Если нужно, чтобы функция вернула не одно значение, а два или более, то для этого функция может вернуть кортеж из двух или нескольких значений:
return (a, b)
Тогда результат вызова функции тоже нужно присваивать кортежу:
(n, m) = f(a, b)
Эпиграф:
def short_story():
print("У попа была собака, он ее любил.")
print("Она съела кусок мяса, он ее убил,")
print("В землю закопал и надпись написал:")
short_story()
Как мы видели выше, функция может вызывать другую функцию. Но функция также может вызывать и саму себя! Рассмотрим это на примере функции вычисления факториала. Хорошо известно, что \(0!=1\), \(1!=1\). А как вычислить величину \(n!\) для большого \(n\)? Если бы мы могли вычислить величину \((n-1)!\), то тогда мы легко вычислим \(n!\), поскольку \(n!=n(n-1)\)!. Но как вычислить \((n-1)!\)? Если бы мы вычислили \((n-2)!\), то мы сможем вычисли и \((n-1)!=(n-1)(n-2)!\). А как вычислить \((n-2)!\)? Если бы... В конце концов, мы дойдем до величины \(0!\), которая равна \(1\). Таким образом, для вычисления факториала мы можем использовать значение факториала для меньшего числа. Это можно сделать и в программе на Питоне:
def factorial (n):
if n == 0:
return 1
else:
return n * factorial(n - 1)
Подобный прием (вызов функцией самой себя) называется рекурсией, а сама функция называется рекурсивной.
Рекурсивные функции являются мощным механизмом в программировании. К сожалению, они не всегда эффективны (об этом речь пойдет позже). Также часто использование рекурсии приводит к ошибкам, наиболее распространенная из таких ошибок – бесконечная рекурсия, когда цепочка вызовов функций никогда не завершается и продолжается, пока не кончится свободная память в компьютере. Пример бесконечной рекурсии приведен в эпиграфе к этому разделу. Две наиболее распространенные причины для бесконечной рекурсии:
if n == 0, то factorial(0) вызовет factorial(-1),
тот вызовет factorial(-2) и т.д.
factorial(n) будет
вызывать factorial(n), то также получиться бесконечная цепочка.
Поэтому при разработке рекурсивной функции необходимо прежде всего оформлять условия завершения рекурсии и думать, почему рекурсия когда-либо завершит работу.
Напишите функцию average(a),
которая получает на вход список чисел и возвращает
среднее значение элементов данного списка.
Список содержит только числа и не пуст.
| Вызов функции | Возвращаемое значение |
|---|---|
average([1, 7, 9]) |
5.666666666666667 |
Напишите функцию median(a, b, c),
которая получает на вход три числа и возвращает
их медиану. В решении нельзя использовать циклы.
| Вызов функции | Возвращаемое значение |
|---|---|
median(1, 9, 7) |
7 |
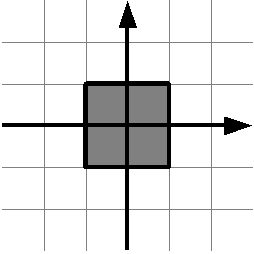
Даны два действительных числа \(x\) и \(y\). Проверьте, принадлежит ли точка с координатами \((x,y)\) заштрихованному квадрату (включая его границу). На рисунке сетка проведена с шагом 1.

Решение оформите в виде функции is_point_in_square(x, y),
возвращающую True, если точка принадлежит квадрату и False, если не принадлежит.
Функция is_point_in_square не должна содержать инструкцию if и должна иметь
такой вид:
def is_point_in_square(x, y):
return ...
| Вызов функции | Возвращаемое значение |
|---|---|
is_point_in_square(0, 0) |
True |
is_point_in_square(3, -7) |
False |
Решите аналогичную задачу для такого квадрата:
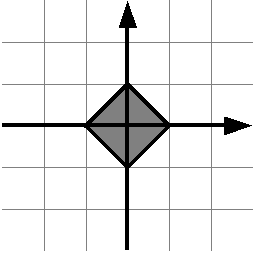
Решение должно соответствовать требованиям для решения задачи C.
Функция должна называться is_point_in_rhombus.
| Вызов функции | Возвращаемое значение |
|---|---|
is_point_in_rhombus(0, 0) |
True |
is_point_in_rhombus(1, 1) |
False |
Даны пять действительных чисел: \(x\), \(y\), \(x_c\), \(y_c\), \(r\). Проверьте, принадлежит ли точка \((x,y)\) кругу с центром \((x_c,y_c)\) и радиусом \(r\).
Решение оформите в виде функции is_point_in_circle(x, y, xc, yc, r).
Решение должно соответствовать требованиям для решения задачи C.
| Вызов функции | Возвращаемое значение |
|---|---|
is_point_in_circle(0.5, 0.5, 0, 0, 1) |
True |
is_point_in_circle(0.5, 0.5, 1, 1, 0.1) |
False |
Проверьте, принадлежит ли точка данной закрашенной области. Область неограничена снизу.
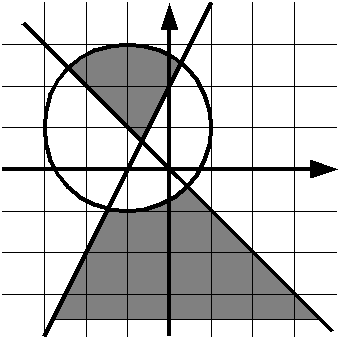
Решение оформите в виде функции is_point_in_area(x, y).
Инструкцию if использовать по-прежнему нельзя.
| Вызов функции | Возвращаемое значение |
|---|---|
is_point_in_area(-1, 2) |
True |
is_point_in_area(0, 0) |
False |
Дано число, получите число, составленное из тех же цифр, записанных в обратном порядке.
Решение оформите в виде функции reverse(n), которая получает
на вход значение типа int и возвращает значение типа int.
| Вызов функции | Возвращаемое значение |
|---|---|
reverse(179) |
971 |
Для данного числа \(n\) определите следующее за ним число, запись которого является палиндромом.
Решение оформите в виде функции next_palindrome(n), которая получает
на вход значение типа int и возвращает значение типа int.
| Вызов функции | Возвращаемое значение |
|---|---|
next_palindrome(179) |
181 |
Дано натуральное число \(n>1\). Найдите его наименьший делитель, отличный от 1.
Решение оформите в виде функции min_divisor(n). Алгоритм должен
иметь сложность \(O(\sqrt{n})\).
Указание. Если у числа \(n\) нет делителя не превосходящего \(\sqrt{n}\), то число \(n\) — простое и ответом будет само число \(n\).
| Вызов функции | Возвращаемое значение |
|---|---|
min_divisor(4) |
2 |
min_divisor(5) |
5 |
Дано натуральное число \(n>1\). Проверьте, является ли оно простым.
Решение оформите в виде функции is_prime(n), которая возвращает
True для простых чисел и False для составных чисел. Решение
должно иметь сложность \(O(\sqrt{n})\).
| Вызов функции | Возвращаемое значение |
|---|---|
is_prime(2) |
True |
is_prime(4) |
False |
Дано натуральное число \(n>1\).
Постройте его разложение на простые множители.
Решение должно быть оформлено в виде функции factor(n), возвращающей список
делителей числа в порядке неубывания. Каждый делитель должен быть включен в список
с учетом его кратности.
Функция должна перебирать делители до \(\sqrt{n}\), при уменьшении числа \(n\) граница перебора также должна уменьшатся.
Использование функций sqrt, pow, операции **
для извлечения квадратного корня может быть причиной долгого работы программы.
Используйте вместо них возведение в квадрат при помощи операции умножения.
| Вызов функции | Возвращаемое значение |
|---|---|
factor(132) |
[2, 2, 3, 11] |
factor(2) |
[2] |
Дано действительное положительное число \(a\) и целое неотрицательное число \(n\).
Вычислите \(a^n\) не используя циклы, стандартную функцию pow,
операцию **, а используя рекуррентное соотношение \(a^n=a\cdot a^{n-1}\).
Решение оформите в виде функции power(a, n).
| Вызов функции | Возвращаемое значение |
|---|---|
power(2, 3) |
8 |
Последовательность Фибоначчи определяется так: \[ \cases{\varphi_0=0, \cr \varphi_1=1, \cr \varphi_{n}=\varphi_{n-1}+\varphi_{n-2} \mbox{, при } n \gt 1.} \]
Напишите функцию fib(n), которая по данному целому неотрицательному n
возвращает \(n\)-e число Фибоначчи.
| Вызов функции | Возвращаемое значение |
|---|---|
fib(6) |
8 |
Запустите программы, вычисляющие числа Фибоначчи при помощи рекурсивного и нерекурсивного алгоритма. Сравните время их работы для n=10, 20, 30, 40, 50. Объясните результат.
Напишите рекурсивную функцию print_numbers(n),
вызов которой приводит к печати на экран натуральных чисел от 1 до \(n\)
по одному числу в строке. Циклы и генераторы списков использовать нельзя.
Подсказка. Число \(n\) является параметром. Как свести задачу “вывести числа от 1 до \(n\)” к задаче с меньшим значением параметра?
| Вызов функции | Вывод |
|---|---|
print_numbers(3) |
1 |
Напишите функцию product(a),
которая по данному списку чисел возвращает произведение
элементов данного списка, не используя циклы.
Список содержит только числа, но может быть пустым.
| Вызов функции | Возвращаемое значение |
|---|---|
product([1, 7, 9]) |
63 |
Дана последовательность целых чисел, заканчивающаяся числом 0. Выведите эту последовательность в обратном порядке. Сделайте это без использования списков и циклов.
Решение оформите в виде функцииreverse(),
не принимающей параметров, которая считывает со стандартного ввода
последовательность чисел до появления числа 0 и выводит эту же последовательность
в обратном порядке. Функция должна считать одно число и, если это число не 0, вызвать
себя рекурсивно.
| Ввод | Вывод |
|---|---|
1 |
0 |
Возводить в степень можно гораздо быстрее, чем за \(n\) умножений! Для этого нужно воспользоваться следующими рекуррентными соотношениями:
\(a^n=(a^2)^{n/2}\) при четном \(n\),
\(a^n=a\cdot a^{n-1}\) при нечетном \(n\).
Реализуйте алгоритм быстрого возведения в степень. Если вы все сделаете правильно, то сложность вашего алгоритма будет \(O(\log n)\).
Решение оформите в виде функции power(a, n). Использовать
стандартную функцию pow и оператор ** по-прежнему запрещается.
| Вызов функции | Возвращаемое значение |
|---|---|
power(1.000000001, 1000000000) |
2.718282030814511 |
Для быстрого вычисления наибольшего общего делителя двух чисел используют алгоритм Евклида. Он построен на следующем соотношении: \(НОД(a,b)=НОД(b,a\bmod b)\).
Реализуйте рекурсивный алгоритм Евклида в виде функции gcd(a, b), возвращающей искомое значение.
| Вызов функции | Возвращаемое значение |
|---|---|
gcd(12, 16) |
4 |
Головоломка “Ханойские башни” состоит из трех стержней, пронумерованных числами 1, 2, 3. На стержень 1 надета пирамидка из \(n\) дисков различного диаметра в порядке возрастания диаметра. Диски можно перекладывать с одного стержня на другой по одному, при этом диск нельзя класть на диск меньшего диаметра. Необходимо переложить всю пирамидку со стержня 1 на стержень 3 за минимальное число перекладываний.
Напишите функцию, которая решает головоломку; для данного числа дисков n
печатает последовательность перекладываний в формате
a b c, где a — номер перекладываемого диска,
b — номер стержня с которого снимается данный диск,
c — номер стержня на который надевается данный диск.
Например, строка 1 2 3 означает перемещение диска номер 1 со стержня
2 на стержень 3. В одной строке печатается одна команда.
Диски пронумерованы числами от 1 до n в порядке возрастания диаметров.
Программа должна вывести минимальный (по количеству произведенных операций) способ перекладывания пирамидки из данного числа дисков.
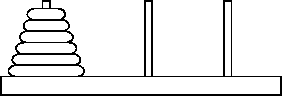
Указание: подумайте, как переложить пирамидку из одного диска? Из двух дисков? Из трех дисков? Из четырех дисков? Пусть мы научились перекладывать пирамидку из \(n\) дисков с произвольного стержня на любой другой, как переложить пирамидку из \(n+1\) диска, если можно пользоваться решением для \(n\) дисков.
Решение оформите в виде функции move(n, start, finish),
которая печатает последовательность перекладываний дисков для перемещения
пирамидки высоты n со стержня номер start
на стержень номер finish.
В примере ниже пирамидка из 2 дисков перекладывается со стержня 1 на стержень 3.
| Вызов функции | Вывод |
|---|---|
move(2, 1, 3) |
1 1 2 |
Постановлением ЮНЕСКО оригинал Ханойской башни был подвергнут реставрации. В связи с этим во время пользования головоломкой нельзя было перекладывать кольца с первого стержня сразу на третий и наоборот.
Решите головоломку с учетом этих ограничений. Вам не нужно находить минимальное решение, но количество совершенных перемещений не должно быть больше 200000, при условии, что количество дисков не превосходит 10.
В этой и последующих задачах на проверку необходимо сдать программу полностью.
Тесты к этой задаче закрытые.
| Ввод | Вывод |
|---|---|
1 |
1 1 2 |
2 |
1 1 2 |
На дорогах Ханоя было введено одностороннее круговое движение, поэтому теперь диск со стержня 1 можно перекладывать только на стержень 2, со стержня 2 на 3, а со стержня 3 на 1.
Решите головоломку с учетом этих ограничений. Вам не нужно находить минимальное решение, но количество совершенных перемещений не должно быть больше 200000, при условии, что количество дисков не превосходит 10.
| Ввод | Вывод |
|---|---|
1 |
1 1 2 |
2 |
1 1 2 |
В Ханое несправедливо запретили класть самый маленький диск (номер 1) на средний колышек (номер 2).
Решите головоломку с учетом этих ограничений. Вам не нужно находить минимальное решение, но количество совершенных перемещений не должно быть больше 200000, при условии, что количество дисков не превосходит 10.
| Ввод | Вывод |
|---|---|
2 |
1 1 3 |
Первоначально все диски лежат на стержне номер 1. Переместите диски с нечетными номерами на стержень номер 2, а с четными номерами - на стержень номер 3.
Вам не нужно находить минимальное решение, но количество совершенных перемещений не должно быть больше 200000, при условии, что количество дисков не превосходит 10.
| Ввод | Вывод |
|---|---|
2 |
1 1 2 |
3 |
1 1 2 |
Как и в предыдущих задачах, дано три стержня, на первом из которых надето \(n\) дисков различного размера. Необходимо их переместить на стержень 3 по следующим правилам:
Самый маленький диск (номер 1) можно в любой момент переложить на любой стержень.
Перемещение диска номер 1 со стержня a на стержень b
будем обозначать 1 a b.
Можно поменять два диска, лежащих на вершине двух стержней, если размеры этих дисков
отличаются на 1. Например, если на вершине стержня с номером a лежит
диск размером 5, а на вершине стержня с номером b лежит диск размером
4, то эти диски можно поменять местами. Такой обмен двух дисков будем обозначать
0 a b (указываются номера стержней, верхние диски которых обмениваются местами).
Для данного числа дисков \(n\), не превосходящего 10, найдите решение головоломки. вам не нужно находить минимальное решение, но количество совершенных перемещений не должно быть больше 200000.
| Ввод | Вывод |
|---|---|
1 |
1 1 3 |
2 |
1 1 3 |
Дана полоска из клеток, пронумерованных от 1 до N слева направо. Разрешено снимать или ставить фишку на клетку с номером 1 или на клетку, следующую за самой левой из установленных фишек. Изначально полоска пуста. Нужно разместить фишки во всех клетках.
Программа получает на вход количество клеток в полоске \(N\) \((1\le N\le 10)\).
Программа должна вывести последовательность номеров клеток, с которыми совершается действие. Если фишка снимается, то номер клетки должен выводиться со знаком минус. Количество действий не должно превышать \(10^4\). Если существует несколько возможных решений задачи, то разрешается вывести любое.
Тесты к этой задаче закрытые.
| Ввод | Вывод |
|---|---|
3 |
1 2 -1 3 1 |
В небоскребе \(n\) этажей. Известно, что если уронить стеклянный шарик с этажа номер \(p\), и шарик разобьется, то если уронить шарик с этажа номер \(p+1\), то он тоже разобьется. Также известно, что при броске с последнего этажа шарик всегда разбивается.
Вы хотите определить минимальный номер этажа, при падении с которого шарик разбивается. Для проведения экспериментов у вас есть два шарика. Вы можете разбить их все, но в результате вы должны абсолютно точно определить этот номер.
Определите, какого числа бросков достаточно, чтобы заведомо решить эту задачу.
Программа получает на вход количество этажей в небоскребе \(n\) и выводит наименьшее число бросков, при котором можно всегда решить задачу.
Тесты к этой задаче закрытые.
| Ввод | Вывод |
|---|---|
4 |
2 |
20 |
6 |
Комментарий к первому примеру. Нужно бросить шарик со 2-го этажа. Если он разобьется, то бросим второй шарик с 1-го этажа, а если не разобьется - то бросим шарик с 3-го этажа.
Подсказки.
1. Как следует действовать, если шарик был бы только один?
2. Пусть шариков два и мы бросили один шарик с этажа номер \(k\). Как мы будем действовать
в зависимости от того, разобьется ли шарик или нет?
3. Пусть f(n) - это минимальное число бросков, за которое можно определить
искомый этаж, если бы в небоскребе было n этажей. Выразите f(n)
через значения f(a) для меньших значений a.