Ctrl+Enter
Так как листок пишется с нуля, то в нём хватает опечаток, неточностей и ошибок. Если вы заметили опечатку или ошибку, выделите её, нажмите Ctrl+Enter и опишите проблему. Желательно также написать ещё и её решение.Точно также можно поступить, если какой-то кусок текста совсем непонятен. А если вы можете предложить замену некоторой части на гораздо более понятный текст — то будет просто замечательно!
PS. Перед тем, как отправить ошибку, обновите страницу. Возможно, ошибка уже исправлена.
PSS. Не нужно тестировать эту функцию просто так, она вроде работает. Но каждое замечание я буду вынужден читать :)
Напоминание
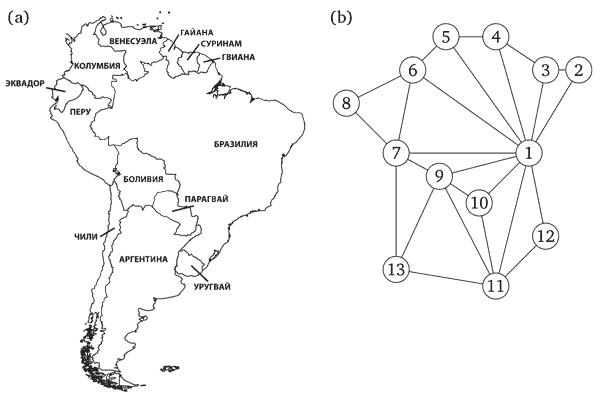
Граф задаётся множеством вершин V и множеством рёбер E, соединяющих пары вершин. (Английская терминология: вершина называется vertex или node, а ребро — edge.)
В примере с картой V = {1, 2, 3, ..., 13}, а рёбра из E соединяют страны, граничащие друг с другом (в частности, E содержит рёбра {1, 2}, {9, 11} и {7, 13}). Отношение «быть соседом» симметрично, так что ребро из x в y возникает одновременно с ребром из y в x. Такие рёбра называются неориентированными (undirected), а соответствующий граф — неориентированным графом (undirected graph).
Бывают и несимметричные отношения, и их изображают ориентированными рёбрами (directed edges). В ориентированном графе наличие ребра из x в y не гарантирует наличие ребра из y в x.
Если явно не указано обратное, то рассматривают только графы без петель (loop) и без кратных рёбер (multiple edge). Такие графы называются простыми (simple).
Самые простые графы — это деревья. Во многих задачах, связанных с графами, используется обходы графа, в результате которых в графе выделяются деревья, состоящие из некоторых вершин графа и некоторых его рёбер. У этих деревьев отмечена вершина, которая называется его корнем (root). Дерево с отмеченной вершиной — корнем — называется корневым деревом (rooted tree).
В корневых деревьях чётко различаются путь к корню и путь от корня. Сосед вершины на пути к корню называется её родителем (parent). Соседи вершины на пути от корня называются её детьми или сыновьими вершинами (child, children). Все вершины на пути из вершины к корню, кроме исходной, называются её предками (ancestor). Все вершины на пути из корня называются потомками (descendant). Вершины, у которых общий родитель, называются братьями (sibling). И наконец вершины, у которых нет потомков, называются листьями (leaf, leaves, terminal vertex).
Представление графа
Рассмотрим граф c \(n = |V|\) вершинами \(v_1,\ldots,v_n\). Его матрицей смежности (adjacency matrix) называется \((n\times n)\)-матрица a, в которой \[ a_{ij} = \begin{cases} 1,&\text{если есть ребро из $v_i$ в $v_j$}\\ 0 &\text{иначе} \end{cases} \] Матрица смежности неориентированного графа, таким образом, симметрична (\(a_{ij} = a_{ji}\)). В таком представлении мы можем за время O(1) проверить, соединены ли данные вершины ребром (посмотрев на один элемент массива). В то же время хранение матрицы требует памяти O(n2), что во многих случаях неэкономно. Альтернативное представление — список смежности (adjacency list). Требуемая при этом память пропорциональна размеру графа (сумме числа вершин и числа рёбер). Элементами списка смежности являются списки, по одному для каждой вершины графа. Для вершины u в таком списке хранятся вершины, в которые ведут рёбра из u, то есть вершины v, для которых \((u, v) \in E\). Для ориентированного графа каждое ребро входит только в один из этих списков (для начальной вершины), а для неориентированного в два (для двух концов ребра). Список смежности, таким образом, требует памяти \(O(|V|+ |E|)\). Проверка наличия ребра \((u, v)\) теперь требует просмотра списка вершины u (что может быть больше O(1) шагов, если вершины хранятся именно в списке, а не в множестве или словаре). Зато в этом представлении легко просмотреть всех соседей заданной вершины (что часто бывает необходимо). Список смежности для неориентированного графа симметричен (если u содержится в списке для v, то и v содержится в списке для u).
Матрица смежности или список смежности?
Что лучше? Ответ зависит от отношения между числом вершин \(|V|\) и числом рёбер \(|E|\). Заметим, что \(|E|\) может быть довольно малым — порядка \(|V|\) (если \(|E|\) сильно меньше \(|V|\), то граф уже вырожденный — в частности, содержит изолированные вершины). Или же довольно большим — порядка \(|V|^2\) (если граф содержит все возможные рёбра). Графы с большим числом рёбер называют плотными (dense), с малым — разреженными (sparse).Выбирая алгоритм, полезно понимать, с какими графами ему в основном придётся иметь дело. Важно это и при хранении: если хранить веб-граф, в котором больше восьми миллиардов вершин, в виде матрицы смежности, то занимать она будет миллионы терабайтов, что сравнимо с общей ёмкостью всех жёстких дисков в мире. И дальше, скорее всего, будет только хуже (матрица может расти быстрее, чем производство дисков). А вот хранить граф Интернета в виде списка смежности вполне разумно, поскольку хранить нужно несколько десятков миллиардов гиперссылок, каждая из которых будет занимать в списке всего несколько байтов, и такого размера диск поместится в карман. Такая разница происходит из-за того, что граф Интернета очень разрежен: страница содержит в среднем пару десятков ссылок на другие страницы — из нескольких миллиардов возможных.
Напоминание про множества и словари
Задание множеств
A = set() # Пустое множество
A = {1, 2, 'hello'} # Явное перечисление элементов
A = set('hello') # Множество букв в строке
B = [1, 2, 1, 2]; A = set(B) # Множество из списка или любого итерируемого объекта
A = {i**2 for i in range(10)} # Генератор множеств
Работа с элементами множеств
C = {1, 2, 'hello'}
for elem in C: # Перебираем все элементы множества
print(elem)
sorted(C) # Список из отсортированных элементов множества
1 in C # Проверка принадлежности
A.add(3) # Добавление элемента
A.remove(3) # Удаление элемента, который есть в множестве
A.discard(4) # Удаление элемента, которого может не быть в множестве
A.pop() # Извлечение случайного элемента из множества с удалением его
Операции с множествами
len(A) # Количество элементов в множестве A | B # Возвращает множество, являющееся объединением множеств A и B. A |= B # Добавляет в множество A все элементы из множества B. A & B # Возвращает множество, являющееся пересечением множеств A и B. A &= B # Оставляет в множестве A только те элементы, которые есть в множестве B. A - B # Возвращает разность множеств A и B (A, но не B). A -= B # Удаляет из множества A все элементы, входящие в B. A ^ B # Возвращает симметрическую разность множеств A и B. A ^= B # Записывает в A симметрическую разность множеств A и B. A <= B # Возвращает true, если A является подмножеством B. A >= B # Возвращает true, если B является подмножеством A. A < B # Эквивалентно A <= B and A != B A > B # Эквивалентно A >= B and A != B
Задание словарей
D = {} # Пустой словарь
D = {1: 'a', 2: 'b'} # Явное перечисление
D = dict([(1, 'a'), (2, 'b')]) # Словарь из списка пар элементов
D = dict(zip([1, 2], ['a', 'b'])) # Словарь из итерируемого объекта, возвращающего пары элементов (ключ-значение)
D = {i: chr(i + ord('a')) for i in range(1, 3)} # Генератор словарей
Работа с элементами словаря
len(D) # Количество элементов в словаре
D[key] # Поиск по ключу, который есть в словаре
key in D # Проверка принадлежности словарю
D[key] = value # Установка или изменение значения
del D[key] # Удаление ключа, который есть в словаре
value = D.pop(key) # Удаления ключа вместе с возвращением значения
value = D.pop(key, no_key_value) # Удаления ключа вместе с возвращением значения. Если ключа нет, то no_key_value
key, value = D.popitem() # Извлечение из словаря пары (ключ, значение) с удалением ключа
D.get(key, no_key_value) # Значение по ключу, no_key_value, если ключа нет
D[key] = D.get(key, 0) + 1 # Самая простая реализация счётчика
for key in D: # Перебираем все ключи
print(key, D[key])
for key, value in D.items(): # Перебираем все пары (ключ, значение)
print(key, value)
for value in D.values(): # Перебор всех значений
print(value)
sorted(D) # Отсортированный список ключей
sorted(D.values()) # Отсортированный список значений
sorted(D.items()) # Отсортированный по ключу список пар (ключ, значение)
sorted(D.items(), key=lambda x: x[1]) # Отсортированный по значению список пар (ключ, значение)
Список смежности и матрица смежности: туда и обратно
01. От матрицы смежности к списку ребер, неориентированный вариант
Простой неориентированный граф задан матрицей смежности, выведите его представление в виде списка ребер.
Входные данные включают число n — количество вершин в графе,
а затем n строк по n чисел, каждое из которых равно 0 или 1, — его матрицу смежности.
Выведите список ребер заданного графа (в любом порядке).
5 0 0 1 0 0 0 0 1 0 1 1 1 0 0 0 0 0 0 0 0 0 1 0 0 0
1 3 2 3 2 5
02. От списка ребер к матрице смежности, неориентированный вариант
Простой неориентированный граф задан списком ребер, выведите его представление в виде матрицы смежности.
Входные данные включают число n — количество вершин в графе, и число m — количество рёбер.
Затем следует m пар чисел — ребра графа. Выведите матрицу смежности заданного графа.
5 3 1 3 2 3 2 5
0 0 1 0 0 0 0 1 0 1 1 1 0 0 0 0 0 0 0 0 0 1 0 0 0
03. От матрицы смежности к списку ребер, ориентированный вариант
Ориентированный граф задан матрицей смежности, выведите его представление в виде списка ребер.
Входные данные включают число n — количество вершин в графе,
а затем n строк по n чисел, каждое из которых равно 0 или 1, — его матрицу смежности.
Выведите список ребер заданного графа (в любом порядке).
5 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0
2 5 3 1 3 2
04. От списка ребер к матрице смежности, ориентированный вариант
Простой ориентированный граф задан списком ребер, выведите его представление в виде матрицы смежности.
Входные данные включают число n — количество вершин в графе, и число m — количество рёбер.
Затем следует m пар чисел — ребра графа. Выведите матрицу смежности заданного графа.
5 3 1 3 2 3 5 2
0 0 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0
Метки времени при обходе в глубину
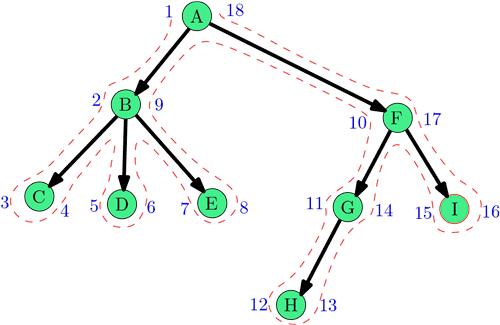Метки времени — приём, который лежит в основе многих применений поиска в глубину.
Обычный алгоритм обхода в глубину описывается рекурсивно: сначала выводим рассматриваемую вершину, а затем для каждого сына выполняем обход в глубину.
Метки времени — это натуральные числа от \(1\) до \(2|V|\). Каждая вершина при обходе в глубину получает две метки: время начала обработки и время окончания, причём все метки всех вершин различны.
Заведём счётчик времени. Изначально счётчик равен нулю. Каждый раз, когда мы переходим от одной вершины к другой мы прибавляем к счётчику единицу. Время начала обработки — это значение счётчика в тот момент, когда мы «выводим рассматриваемую вершину». Время окончания — это значение счётчика после того, как будет выполнен обход в глубину для всех сыновьих вершин. Каждый раз, когда мы начинаем обход для какой-либо вершины, мы прибавляем 1 к счётчику. Аналогично мы прибавляем 1 к счётчику после того, как закончили обход для данной вершины.
На картинке справа приведён обход в глубину с отметками времени. Дополнительно простановку меток времени можно представлять себе так: нарисуем дерево на плоскости, после чего обведём его пунктиром начиная с корня. Каждый раз, когда наш пунктир проходит слева или справа от вершины, мы записываем число — порядковый номер встречи с вершиной. Числа, записанные слева от каждой вершины будут временем начала обработки, числа справа — временем окончания.
Заметим сначала довольно банальное свойство меток времени: если отсортировать все вершины по возрастанию времени начала обработки или по убыванию времени окончания обработки, то получившийся порядок будет соответствовать некоторому обходу в глубину.
Следующее свойство — времена начала и окончания образуют правильную скобочную структуру. Если мы в последовательности чисел от \(1\) до \(2|V|\) заменим числа, соответствующие меткам начала обработки на открывающую скобку, а числа, соответствующие меткам окончания обработки на закрывающую, то в результате получится правильная скобочная структура. Так в примере выше получается \[ \mathbf{(\ (\ (\ )\ (\ )\ (\ )\ )\ (\ (\ (\ )\ )\ (\ )\ )\ )} \]
Дальше: оказывается, по меткам времени очень легко понять, является ли одна вершина предком другой или наоборот. Как? Ну, это вы сами должны догадаться.
Когда мы будем работать с более сложными графами, то увидим ещё несколько применений меткам времени.
05. Метки времени при обходе в глубину дерева
На вход подаётся корневое дерево в формате задач 01 и 02 из предыдущего листка. Выполните обход дерева в глубину начиная с корня и вычислите метки времени для вашего обхода. Выведите вершины в лексикографическом порядке, указав для каждой вершины время начала и время окончания обработки.
(Конкретные времена зависят от обхода и могут не совпадать с временами в примере)
Для решения могут пригодиться глобальные переменные. Напоминание здесь.
9 B A C B D B E B F A G F H G I F
A 1 18 B 2 9 C 3 4 D 5 6 E 7 8 F 10 17 G 11 14 H 12 13 I 15 16
Для решения нужно "усилить" самый обычный рекурсивный обход в глубину.
Нужно создать глобальные переменные time=0, time_in={} и time_out={}.
В начале функции нужно прибавлять к времени 1 и заносить время в словарь time_in,
после обхода всех сыновьих вершин нужно прибавлять к времени 1 и заносить время в словарь time_out.
Несложно модифицировать и нерекурсивный алгоритм на основе стека.
Идея будет следующей: после того, как мы сняли вершину со стека, нужно проверить, если ли она в словаре time_in.
Если есть, то выбросить её и идти дальше. А если нет, то добавить метку времени, ещё раз добавить её в стек и начать обходить её сыновьи вершины.
После того, как все они будут обработаны, мы снова вернёмся к этой вершине и проставим время окончания обработки.
06. Предки и потомки — 2
Даны два элемента в дереве. Определите, является ли один из них потомком другого.
Программа получает на вход описание дерева. Далее идёт натуральное число M — количество запросов. После этого идёт M строк, содержащие имена двух элементов дерева. Для каждого такого запроса выведите одно из трех чисел: 1, если первый элемент является предком второго (или они совпадают), 2, если второй является предком первого или 0, если ни один из них не является предком другого. Число M будет очень велико, поэтому каждая такая проверка должна требовать константу времени. Для этого можно использовать метки времени из предыдущей задачи.
4 Alice Jake Caitlin Jake Grace Alice 3 Alice Jake Jake Alice Alice Caitlin
2 1 0
Как хранить графы в программе
В графе в отличие от корневого дерева нет корня и нет разницы между предками и потомками. Все рёбра равнозначны. Поэтому удобно хранить граф в виде словаря, ключами которого являются все вершины, а значениями — множество вершин, соединённых с данной. Если граф неориентированный, то каждое ребро(v, w) "хранится" сразу в двух множествах.
Пока мы будем иметь дело только с простыми графами без изолированных вершин, поэтому каждая вершина участвует в каком-то ребре. Поэтому множество всех вершин графа будет определяться как множество вершин всех рёбер.
07. digraph_from_input()
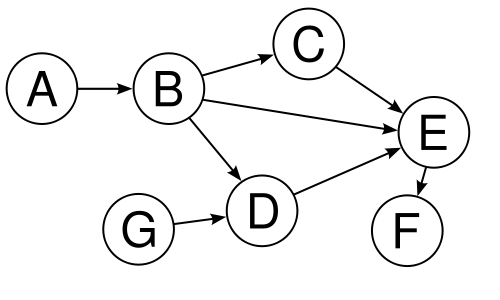
Программа получает на вход число рёбер в ориентированном графе N.
Далее следует N строк, задающие рёбра графа.
Каждая строка имеет вид откуда_ребро куда_ребро.
Программа должна сформировать словарь digraph смежности ориентированного графа
и вывести его при помощи функции pprint из модуля pprint.
Реализуйте функцию digraph_from_input(), которая считывает граф в таком формате из стандартного ввода
и возвращает словарь digraph.
8 A B B C B D B E C E D E E F G D
{'A': {'B'},
'B': {'C', 'E', 'D'},
'C': {'E'},
'D': {'E'},
'E': {'F'},
'F': set(),
'G': {'D'}}
08. graph_from_input()
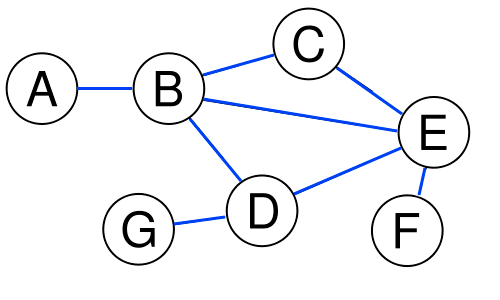
Программа получает на вход число рёбер в неориентированном графе N.
Далее следует N строк, задающие рёбра графа.
Каждая строка имеет вид откуда_ребро куда_ребро.
Программа должна сформировать словарь graph смежности неориентированного графа
и вывести его при помощи функции pprint из модуля pprint.
Реализуйте функцию graph_from_input(), которая считывает граф в таком формате из стандартного ввода
и возвращает словарь graph.
8 A B B C B D B E C E D E E F G D
{'A': {'B'},
'B': {'A', 'C', 'E', 'D'},
'C': {'B', 'E'},
'D': {'B', 'E', 'G'},
'E': {'C', 'B', 'D', 'F'},
'F': {'E'},
'G': {'D'}}
09. Степень вершины
Дан неориентированный граф.
Выведите степень каждой вершины. Вершины должны выводиться в лексикографическом порядке.
8 A B B C B D B E C E D E E F G D
A 1 B 4 C 2 D 3 E 4 F 1 G 1
10. Эйлеров цикл в связном графе
Дан связный неориентированный граф.
Выведите YES, если в нём есть эйлеров цикл, и NO иначе.
8 A B B C B D B E C E D E E F G D
NO
3 A B B C C A
YES
11. Из орграфа в графы
Ориентированный граф кратко называется орграфом. Для краткости далее под графом всегда будет пониматься только неориентированный граф.
Из орграфа всегда можно сделать граф, убрав стрелочки с вершин.
На вход подаётся строка, в которой записан словарь digraph.
Его можно записать в переменную при помощи кода
digraph = eval(input())Сделайте из этого орграфа неориентированный граф и выведите его при помощи
pprint.
{'A': {'B'}, 'B': {'C', 'D', 'E'}, 'C': {'E'}, 'D': {'E'}, 'E': {'F'}, 'F': set(), 'G': {'D'}}
{'A': {'B'},
'B': {'A', 'C', 'E', 'D'},
'C': {'B', 'E'},
'D': {'B', 'E', 'G'},
'E': {'C', 'B', 'D', 'F'},
'F': {'E'},
'G': {'D'}}
12. Входящая и исходящая степень вершины
Дан ориентированный граф.
Выведите входящую (количество входящих рёбер, indegree) и исходящую (количество исходящих рёбер, outdegree) степень каждой вершины. Вершины должны выводиться в лексикографическом порядке.
8 A B B C B D B E C E D E E F G D
A 0 1 B 1 3 C 1 1 D 2 1 E 3 1 F 1 0 G 0 1
13. Квадрат орграфа
Дан ориентированный граф.
Квадратом графа называется граф с тем же множеством вершин, что и исходный, но в котором из вершины v проведено ребро в w, если в исходном графе из вершины v можно попасть в w не более, чем за 2 шага.
8 A B B C B D B E C E D E E F G D
{'A': {'C', 'B', 'E', 'D'},
'B': {'C', 'E', 'D', 'F'},
'C': {'E', 'F'},
'D': {'E', 'F'},
'E': {'F'},
'F': set(),
'G': {'E', 'D'}}
14. Транспонирование орграфа
Дан ориентированный граф.
Транспонированным графом называется граф с тем же множеством вершин, что и исходный, но в котором из вершины v проведено ребро в w тогда и только тогда, когда в исходном графе есть ребро из w в v.
На вход подаётся строка, в которой записан словарь digraph.
Транспонируйте этот орграф и выведите его при помощи pprint.
{'A': {'B'}, 'B': {'C', 'D', 'E'}, 'C': {'E'}, 'D': {'E'}, 'E': {'F'}, 'F': set(), 'G': {'D'}}
{'A': set(),
'B': {'A'},
'C': {'B'},
'D': {'B', 'G'},
'E': {'C', 'B', 'D'},
'F': {'E'},
'G': set()}
15. Обратный граф
Дан неориентированный граф.
Дополнением или обратным графом называется граф с тем же множеством вершин, что и исходный, но в котором из вершины v проведено ребро в w тогда и только тогда, когда в исходном графе нет ребра из v в w.
На вход подаётся граф в формате из задачи 08.
Создайте обратный граф и выведите его при помощи pprint.
8 A B B C B D B E C E D E E F G D
{'A': {'C', 'E', 'D', 'G', 'F'},
'B': {'G', 'F'},
'C': {'A', 'D', 'G', 'F'},
'D': {'A', 'C', 'F'},
'E': {'A', 'G'},
'F': {'A', 'C', 'B', 'D', 'G'},
'G': {'A', 'C', 'B', 'E', 'F'}}
16. Обход в ширину
Дан ориентированный граф и одна из его вершин.
Выполните обход графа в ширину начиная с этой вершины.
Сложность получившегося алгоритма должна быть \(O(|V| + |E|)\).
8 A B B C B D B E C E D E E F G D A
A B C E D F
Здесь нужно делать всё также, как и для деревьев, только дополнительно нужно хранить множество посещённых вершин и не ходить в них повторно.
Есть два самых простых способа делать такой обход: при помощи слоёв или при помощи очереди. В разных случаях конкретный способ может быть удобнее благодаря некоторым бонусам.
Решение при помощи слоёв:
Будем хранить два множества: множество элементов, которые необходимо обойти на текущем уровне дерева, а также множество встреченных элементов следующего уровня.
Сначала добавляем в первое множество начальную вершину, а второе оставляем пустым. Далее до тех пор, пока первое множество не иссякнет выполняем процедуру обхода: для каждого элемента первого множества выводим его, после чего добавляем всех его потомков во второе множество. После того, как все элементы первого множества будут обработаны, назначаем второе множество первым, а пустое множество — новым вторым.
Решение при помощи слоёв удобно для вычисления минимальных расстояний, количества кратчайших путей или просто путей и подобных задач.
Решение при помощи очереди.
Воспользуемся деком из модуля collections, он позволяет эффективно добавлять элементы слева списка, а забирать — справа.
Такая структура данных называется очередью.
Добавим начальную вершину в очередь.
Множество посещённых вершин пока пусто.
Пока очередь не пуста будем выполнять простое действие: снимаем вершину с очереди, выводим её, добавляем в множество посещённых.
И добавляем всех её ещё не посещённых соседей в очередь.
Решение при помощи очереди хорошо обобщается на графы с разной стоимостью рёбер.
Например, поиск коротких путей в 0-1 графах (см. задачу ниже) делается из обычного обхода буквально в пару строчек.
Пример операций с очередью:
from collections import deque queue = deque([start_node]) visit = queue.pop() queue.appendleft(next_node)
17. Обход в глубину
Дан ориентированный граф и одна из его вершин.
Выполните обход графа в глубину начиная с этой вершины.
Сложность получившегося алгоритма должна быть \(O(|V| + |E|)\).
8 A B B C B D B E C E D E E F G D A
A B С E F D
Здесь нужно делать всё также, как и для деревьев, только дополнительно нужно хранить множество посещённых вершин и не ходить в них повторно.
Есть три самых распространённых способа выполнения обхода в глубину. Как обычно в разных случаях конкретный способ может быть удобнее благодаря некоторым бонусам.
Решение при помощи рекурсии:
Это самое простое с точки зрения реализации решение.
Стартуем с начальной вершины.
Проверяем, посещена ли текущая вершина. Если посещена, то заканчиваем обход.
Если ещё нет, по посещаем (выводим и добавляем в множество посещённых вершин), после чего рекурсивно применяем процедуру
ко всем ещё не посещённым соседям.
Само решение достаточно простое, и его легко модифицировать так, чтобы получать отметки времени входа и выхода.
В решении нужно не забыть увеличить максимальную глубину рекурсии.
Решение при помощи стека.
Добавляем начальную вершину в стек (в Python'е — в обычный список при помощи append),
а также в множество посещённых вершин.
Далее работаем в цикле пока стек не пуст:
снимаем вершину со стека (в Python'е — при помощи pop).
Проверяем, посещена ли она.
Если ещё нет, по посещаем (выводим и добавляем в множество посещённых вершин), после чего добавляем в стек всех ещё не посещённых соседей.
Решение удобно своей краткостью, простотой и эффективностью, однако его достаточно дополнять фичами.
Решение при помощи стека и покраски вершин.
Будем обходить граф и попутно красить вершины.
Цвет вершины будем хранить в словаре.
Изначально все вершины белые — это значит, мы с этими вершинами ещё ни разу не сталкивались.
Будем использовать стек, в котором в каждый момент времени будет храниться путь из начальной вершины до текущей,
а также множество ещё необработанных соседей каждой вершины в стеке.
Кладём в стек пару из начальной вершины и множества её соседей, после чего красим её в серый цвет.
Серый цвет означает, что мы уже встречали эту вершину, но ещё не обошли в глубину всех её соседей.
Дальше пока стек не пуст выполняем:
Смотрим на вершину стека.
Если в множество соседей для обработки пусто,
то красим вершину в чёрный цвет (что означает, что все соседи данной вершины уже пройдены),
после чего удаляем её (вместе с уже пустым множеством её необработанных соседей) из стека.
Если же множество ещё непусто, то изымаем из него очередную вершину.
Если она белая, то красим её в серый и добавляем в стек её и множество её соседей. Иначе игнорируем её.
Такое решение удобно и для вычисления отметок весов (время входа — момент покраски в серый, времы выхода — в чёрный),
для классификации рёбер на древесные, прямые, обратные и перекрёстные.
В таком решении легко вывести путь из корня до текущей вершины (нужно просто пройти по стеку).
В таком решении удобно искать циклы: если при обработке множества необработанных соседей мы встретили серую вершину,
то тем самым нашли цикл, так как серые вершины — это в точности вершины в нашем стеке.
А ещё с помощью такого решения удобно делать топологическую сортировку.
18. Достижимость
Дан ориентированный граф и несколько пар его вершин.
Выведите 'YES', если существует путь из первой вершины пары во вторую и 'NO' иначе.
Сложность проверки для каждой пары вершин должна быть не больше \(O(|V| + |E|)\).
8 A B B C B D B E C E D E E F G D 3 A B A F A G
YES YES NO
Нужно просто сделать обход в глубину или в ширину начиная с первой вершины. Если в пути встретится вторая вершина, то она достижима, иначе — нет.
19. Минимальное расстояние до вершины
Дан ориентированный граф и отмечена одна из его вершин.
Для каждой вершины графа выведите длину минимального пути из отмеченной. Если такого пути нет, то выведите -1. Вершины должны выводиться в лексикографическом порядке.
Сложность получившегося алгоритма должна быть \(O(|V| + |E|)\).
Здесь удобно сделать обход в ширину по слоям (см. подсказку к обходу в ширину). При этом мы для каждого слоя будем в словаре сохранять его расстояние до начальной вершины.
8 A B B C B D B E C E D E E F G D A
A 0 B 1 C 2 D 2 E 2 F 3 G -1
20. Количество компонент связности
Дан неориентированный граф.
Выведите количество его компонент связности.
Сложность получившегося алгоритма должна быть \(O(|V| + |E|)\).
8 A B B C B D B E C E D E E F G D
1
3 A B C D E F
3
Идея снова очень проста: берём вершину и делаем из неё обход в ширину или в глубину. Все посещённые вершины дают компоненту связности. Дальше нужно брать ещё непосещённую вершину и повторять до тех пор, пока все вершины будут посещены.
21. Дерево поиска в ширину
Дан ориентированный граф и одна из его вершин.
Выполним обход в ширину начиная с этой вершины.
Рассмотрим множество рёбер, после прохода по которым мы попадали в новую вершину.
Они образуют корневое дерево с корнем в исходной вершине.
Выведите словарь parents этого корневого дерева.
Сложность получившегося алгоритма должна быть \(O(|V| + |E|)\).
8 A B B C B D B E C E D E E F G D A
{'A': None, 'B': 'A', 'C': 'B', 'D': 'B', 'E': 'B', 'F': 'E'}
Достаточно легко модифицируется любой вариант обхода в ширину.
Каждый раз, когда мы "посещаем" вершину во время обхода в ширину, нужно добавить её предка в словарь.
Отдельно нужно добавить запись для корня (с ссылкой на Node).
22. Самые короткие пути
Дан ориентированный граф и отмечена одна из его вершин V.
Далее перечисляются несколько вершин этого графа. Для каждой вершины W выведите какой-нибудь из самых коротких путей из вершины V в вершину W, и -1 если такого пути нет.
Сложность подготовки должна быть \(O(|V| + |E|)\). Сложность нахождения какой-нибудь из самых коротких путей после подготовки должна быть порядка длины этого пути.
8 A B B C B D B E C E D E E F G D A 3 B F G
A B A B E F -1
Это — очень красивое применение дерева обхода в ширину. Один из самых коротких путей всегда будет по дереву обхода в ширину, так уж оно устроено :) Имея дерево обхода очень легко найти путь от него к корню, после чего обратить его.
23. Дерево поиска в глубину
Дан ориентированный граф и одна из его вершин.
Выполним обход в глубину начиная с этой вершины.
Рассмотрим множество рёбер, после прохода по которым мы попадали в новую вершину.
Они образуют корневое дерево с корнем в исходной вершине.
Выведите словарь parents этого корневого дерева.
Сложность получившегося алгоритма должна быть \(O(|V| + |E|)\).
8 A B B C B D B E C E D E E F G D A
{'A': None, 'B': 'A', 'C': 'B', 'D': 'B', 'E': 'С', 'F': 'E'}
Достаточно легко модифицируется любой вариант обхода в глубину.
Каждый раз, когда мы "посещаем" вершину во время обхода в глубину, нужно добавить её предка в словарь.
Отдельно нужно добавить запись для корня (с ссылкой на Node).
24. Цикл в графе
Дан неориентированный граф.
Если в графе есть цикл, то выведите 'YES' и вершины любого цикла. В противном случае выведите 'NO'.
Сложность получившегося алгоритма должна быть \(O(|V| + |E|)\).
8 A B B C B D B E C E D E E F G D
YES B C E D
3 A B B C C D
NO
И эта задача решается при помощи обхода. Выполняем обход в глубину или в ширину, сохраняя при этом дерево обхода (см. соответствующие задачи). Как только очередное ребро смотрит в посещённую вершину — мы получили цикл. Проще всего его получить пройдя от этих вершин до их наименьшего общего предка (или прямо до корня).
25. Цикл в орграфе
Дан ориентированный граф.
Если в графе есть цикл, то выведите 'YES' и вершины любого цикла. В противном случае выведите 'NO'.
Сложность получившегося алгоритма должна быть \(O(|V| + |E|)\).
8 A B B C B D B E C E D E E F G D
NO
3 A B B C C A
YES A B C
26. Топологическая сортировка
Дан ориентированный граф без циклов. Необходимо вывести всего его вершины в таком порядке, чтобы из любой вершины с б́ольшим номером не существовало пути ни в какую вершину с м́еньшим номером.
Сложность получившегося алгоритма должна быть \(O(|V| + |E|)\) или \(O(\log(|V|)\cdot(|V| + |E|))\).
8 A B B C B D B E C E D E E F G D
G A B C D E F
27. Количество путей
Дан ациклический ориентированный граф и несколько пар его вершин. Определите количество простых путей (то есть путей, все рёбра которого попарно различны) и одной вершины в другую.
Сложность получившегося алгоритма не считая сложности арифметических операций должна быть \(O(|V| + |E|)\). (Например, количество путей в полном графе будет порядка \(n!\), для больших \(n\) арифметические операции с такими числами занимают существенное время)
8 A B B C B D B E C E D E E F G D 3 B E B A G F
3 0 1
28. Кратчайший путь в 0-1-графе
Имеется схема городского транспорта (неориентированный граф), в котором участвую автобусы и троллейбусы. Проезд на автобусе стоит 1$, проезд на троллейбусе бесплатен. Необходимо найти какой-нибудь самый дешёвый способ добраться от одной остановки до другой. Если такого пути нет, то выведите -1.
Сложность получившегося алгоритма должна быть \(O(|V| + |E|)\).
7 A B 1 B C 0 C D 1 A F 0 F E 1 E D 0 L M 0 3 A D B C A L
A F E D B C -1
29. Кратчайший цикл
Дан ориентированный граф. Необходимо вывести любой из кратчайших циклов. Если ни одного цикла нет, то выведите -1.
Сложность получившегося алгоритма должна быть \(O(|V|\cdot(|V| + |E|))\).
7 A B B C C D D E B F F E E A
A B F E A
30. Кратчайший чётный путь
Дан ориентированный граф и несколько пар его вершин. Выведите кратчайший путь чётной длины от одной вершины до другой, или -1, если такого пути нет.
Сложность получившегося алгоритма должна быть \(O(|V| + |E|)\).
6 A E A B B D B C C D D E 2 A E C B
A B C D E -1
31. Рёбра на кратчайшем пути
Дан неориентированный граф и две его вершины. Выведите все рёбра, которые лежат на каком-либо кратчайшем пути от одной вершины до другой.
Сложность получившегося алгоритма должна быть \(O(|V| + |E|)\).
6 A E A B B D B C C D D E B E
A B A E B D D E
32. Вершины на кратчайшем пути
Дан неориентированный граф и две его вершины. Выведите все вершины, которые лежат на каком-либо кратчайшем пути от одной вершины до другой (не считая начальной и конечной вершины).
Сложность получившегося алгоритма должна быть \(O(|V| + |E|)\).
6 A E A B B D B C C D D E B E
A D
33. Компоненты сильной связности
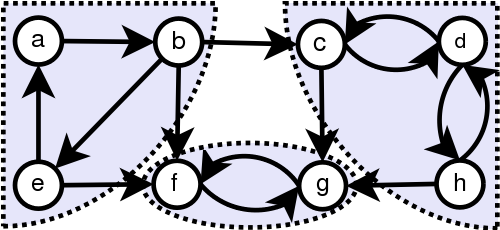
Дан ориентированный граф. Подмножество его вершин называется компонентой сильной связности, если между любыми двумя вершинами существует путь в графе, и в то же время ни одна другая вершина не может быть добавлена с сохранением этого свойства.
Выведите количество компонент сильной связности, а затем — список вершин каждой компонты через пробел. Отсортируйте вершины каждой компоненты в лексикографическом порядке, а сами компоненты — в порядке возрастания "минимальной" вершины.
Сложность получившегося алгоритма должна быть \(O(|V| + |E|)\).
14 a b b e e a b f e f f g g f b c c g c d d c d h h d h g
3 a b e c d h f g
3 A B B C C D
4 A B C D
7 A B B C C A B M M N N P P M
2 A B C M N P
34. Поиск мостов
Дан неориентированный граф. Его ребро называется мостом или перешейком, если после его удаления количество компонент связности увеличивается. Эквивалентное определение — ребро является мостом в том и только в том случае, если оно не содержится ни в одном цикле.
Выведите список мостов графа, отсортированный в лексикографическом порядке (вершины каждого ребра тоже солжны быть упорядочены).
Сложность получившегося алгоритма должна быть \(O(|V| + |E|)\).
8 A B B C B D B E C E D E E F G D
A B D G E F
3 A B B C C D
A B B C C D
7 A B B C C A B M M N N P P M
B M
35. Поиск точек сочленения
Дан неориентированный граф. Его вершина называется шарниром или точкой сочленения, если после её удаления количество компонент связности увеличивается.
Выведите список точек сочленения, отсортированный в лексикографическом порядке.
Сложность получившегося алгоритма должна быть \(O(|V| + |E|)\).
8 A B B C B D B E C E D E E F G D
B D E
3 A B B C C D
B C
7 A B B C C A B M M N N P P M
B M