Напишите функцию int min(int a, int b, int c, int d), вычисляющую минимум четырех чисел, которая
не содержит инструкции if, а использует стандартную функцию min от двух аргументов.
Ваша функция должна содержать только одну инструкцию return и в ней не должно быть
операций присваивания и вспомогательных переменных. Считайте четыре целых числа и выведите их минимум.
| Ввод | Вывод |
|---|---|
5 |
1 |
Даны четыре действительных числа: \(x_1\), \(y_1\), \(x_2\), \(y_2\). Напишите функцию
double dist(double x1, double y1, double x2, double y2), вычисляющую расстояние
между точкой \((x_1,y_1)\) и \((x_2,y_2)\). Считайте четыре действительных числа
и выведите результат работы этой функции.
| Ввод | Вывод |
|---|---|
0 |
1.4142135623730951 |
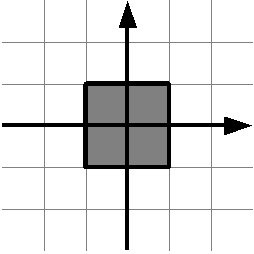
Даны два действительных числа \(x\) и \(y\). Проверьте, принадлежит ли точка с координатами
\((x,y)\) заштрихованному квадрату (включая его границу). Если точка принадлежит квадрату, выведите слово YES,
иначе выведите слово NO. На рисунке сетка проведена с шагом 1.

Решение должно содержать функцию bool is_point_in_square(double x, double y),
возвращающую true, если точка принадлежит квадрату и false, если не принадлежит.
Основная программа должна считать координаты точки, вызвать функцию is_point_in_square
и в зависимости от возвращенного значения вывести на экран необходимое сообщение.
Функция is_point_in_square не должна содержать инструкцию if.
| Ввод | Вывод |
|---|---|
0 |
YES |
3 |
NO |
Решите аналогичную задачу для такого квадрата:
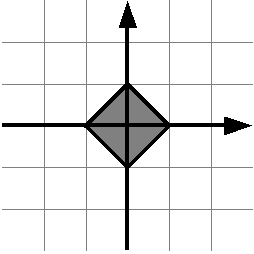
Решение должно соответствовать требованиям для решения задачи C.
| Ввод | Вывод |
|---|---|
0 |
YES |
1 |
NO |
Даны пять действительных чисел: \(x\), \(y\), \(x_c\), \(y_c\), \(r\). Проверьте, принадлежит ли точка \((x,y)\) кругу с центром \((x_c,y_c)\) и радиусом \(r\).
Решение оформите в виде функции bool is_point_in_circle(double x, double y, double xc, double yc, double r).
Решение должно соответствовать требованиям для решения задачи C.
| Ввод | Вывод |
|---|---|
0.5 |
YES |
0.5 |
NO |
Проверьте, принадлежит ли точка данной закрашенной области:
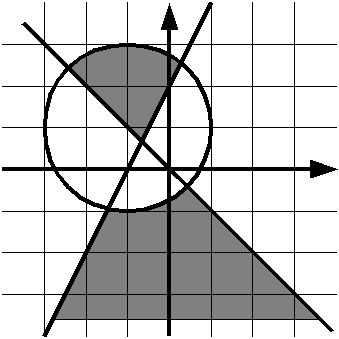
Решение оформите в виде функции bool is_point_in_area(double x, double y).
Решение должно соответствовать требованиям для решения задачи С.
| Ввод | Вывод |
|---|---|
-1 |
YES |
0 |
NO |
Дано натуральное число \(n>1\). Выведите его наименьший делитель, отличный от 1.
Решение оформите в виде функции int min_divisor(int n). Алгоритм должен
иметь сложность \(O(\sqrt{n})\).
Указание. Если у числа \(n\) нет делителя не превосходящего \(\sqrt{n}\), то число \(n\) — простое и ответом будет само число \(n\).
| Ввод | Вывод |
|---|---|
4 |
2 |
5 |
5 |
Дано натуральное число \(n>1\). Проверьте, является ли оно простым. Программа должна вывести слово
YES, если число простое и NO, если число составное.
Решение оформите в виде функции bool is_prime(int n), которая возвращает
true для простых чисел и false для составных чисел. Решение
должно иметь сложность \(O(\sqrt{n})\).
| Ввод | Вывод |
|---|---|
2 |
YES |
4 |
NO |
Напишите функцию void Swap(int & a, int & b),
обменивающую значения переменных a и b и не использующую дополнительную
вспомогательную переменную.
Сдайте программу, меняющую местами значения двух целочисленных переменных.
| Ввод | Вывод |
|---|---|
1 2 |
2 1 |
Swap без вспомогательной переменнойВозьмите функцию Swap из предыдущей задачи и добавьте к ней функцию main:
int main()
{
int a = 179;
Swap(a, a);
cout << a << endl;
return 0;
}
Запустите программу. Подумайте, почему она вывела такой результат.
Даны два натуральных числа \(n\) и \(m\). Сократите дробь \(\frac{n}{m}\), то есть выведите два других числа \(p\) и \(q\) таких, что \(\frac{n}{m}=\frac{p}{q}\) и дробь \(\frac{p}{q}\) — несократимая.
Решение оформите в виде функции
void reduce_fraction(int & n, int & m),
получающая значения n и m по ссылке и изменяющая их.
| Ввод | Вывод |
|---|---|
12 16 |
3 4 |
Мнение конструкторов ЭВМ и математиков о том, что такое деление с остатком для отрицательных чисел расходится. Напомним, что при делении числа \(a\) на число \(b\) с остатком находятся такие числа \(q\) (частное) и \(r\) (остаток), что \(a=qb+r\). При этом \(|r|<|b|\). Если числа \(a\) и \(b\) — положительные, то выполняется более сильное неравенство: \(0 \le r < b\) и тогда деление с остатком определяется однозначно. Но если числа — отрицательные то деление с остатком на компьютере выполняется не так, как это кажется правильным математикам.
Вот как выполняется деление с остатком на компьютере для отрицательных чисел:
a |
b |
a / b |
a % b |
|---|---|---|---|
26 |
10 |
2 |
6 |
-26 |
10 |
-2 |
-6 |
26 |
-10 |
-2 |
6 |
-26 |
-10 |
2 |
-6 |
Таким образом, в компьютере целочисленное частное является результатом округления действительного частного
в сторону нуля, как это делает функция trunc. Между тем, математик считает, что целочисленное
частное — это целая часть от частного \((q=\lfloor a/b\rfloor)\), то есть результат использования функции floor.
Это даст такие результаты с точки зрения математики:
| \(a\) | \(b\) | \(\lfloor a / b\rfloor\) | \(a \bmod b\) |
|---|---|---|---|
26 |
10 |
2 |
6 |
-26 |
10 |
-3 |
4 |
26 |
-10 |
-3 |
-4 |
-26 |
-10 |
2 |
-6 |
Напишите программу, которая по данным числам \(a\) и \(b\) вычисляет их целочисленное частное и остаток от деления так, как это принято в математике. Программа не должна использовать действительные числа и циклы.
Решение оформите в виде функции void div_mod(int a, int b, int & q, int & r), где
a — делимое, b — делитель,
q — переменная для записи частного, r — переменная
для записи остатка.
| Ввод | Вывод |
|---|---|
-26 10 |
-3 4 |
26 -10 |
-3 -4 |
Дано действительное положительное число \(a\) и целое неотрицательное число \(n\).
Вычислите \(a^n\) не используя циклы и стандартную функцию pow, а используя
рекуррентное соотношение \(a^n=a\cdot a^{n-1}\).
Решение оформите в виде функции double power(double a, int n).
| Ввод | Вывод |
|---|---|
2 |
8 |
Напишите рекурсивную функцию int sum(int a, int b), возвращающую
сумму двух целых неотрицательных чисел. Из всех арифметических операций допускаются
только + 1 и - 1. Также нельзя использовать циклы.
| Ввод | Вывод |
|---|---|
2 |
4 |
Последовательность Фибоначчи определяется так: \[ \varphi_0=0, \varphi_1=1, ..., \varphi_{n}=\varphi_{n-1}+\varphi_{n-2}. \]
Напишите функцию int fib(int n), которая по данному целому неотрицательному n
возвращает \(n\)-e число Фибоначчи.
| Ввод | Вывод |
|---|---|
6 |
8 |
Запустите программы, вычисляющие числа Фибоначчи при помощи рекурсивного и нерекурсивного алгоритма. Сравните время их работы для n=10, 20, 30, 40, 50. Объясните результат.
Дана последовательность чисел, завершающаяся числом 0. Найдите сумму всех этих чисел, не используя цикл. В этой задаче нельзя пользоваться списками и строками для сохранения всех введенных чисел.
Указание. Программа должна содержать функцию int sum(),
не принимающую параметров, которая возвращает (при помощи
return) значение суммы считанных со стандартного
ввода чисел. Сама функция при этом результат не выводит на стандартный вывод.
| Ввод | Вывод |
|---|---|
1 |
17 |
Дана последовательность целых чисел, заканчивающаяся числом 0. Выведите эту последовательность в обратном порядке.
| Ввод | Вывод |
|---|---|
1 |
0 |
Указание. Программа должна содержать функцию void reverse(),
не принимающую параметров, которая считывает последовательность
чисел и выводит эту же последовательность в обратном порядке на стандартный вывод.
Попробуйте решить предыдущую задачу без использования вспомогательной функции.
А что, main() не функция что-ли?
Возводить в степень можно гораздо быстрее, чем за \(n\) умножений! Для этого нужно воспользоваться следующими рекуррентными соотношениями:
\(a^n=(a^2)^{n/2}\) при четном \(n\),
\(a^n=a\cdot a^{n-1}\) при нечетном \(n\).
Реализуйте алгоритм быстрого возведения в степень. Если вы все сделаете правильно, то сложность вашего алгоритма будет \(O(\log n)\).
| Ввод | Вывод |
|---|---|
1.000000001 |
2.7182820387553908 |
Для быстрого вычисления наибольшего общего делителя двух чисел используют алгоритм Евклида. Он построен на следующем соотношении: \(НОД(a,b)=НОД(a\bmod b,b)\).
Реализуйте рекурсивный алгоритм Евклида в виде функции int gcd(int a, int b).
| Ввод | Вывод |
|---|---|
12 |
4 |
Головоломка “Ханойские башни” состоит из трех стержней, пронумерованных числами 1, 2, 3. На стержень 1 надета пирамидка из \(n\) дисков различного диаметра в порядке возрастания диаметра. Диски можно перекладывать с одного стержня на другой по одному, при этом диск нельзя класть на диск меньшего диаметра. Необходимо переложить всю пирамидку со стержня 1 на стержень 3 за минимальное число перекладываний.
Напишите программу, которая решает головоломку; для данного числа дисков n
печатает последовательность перекладываний в формате
a b c, где a — номер перекладываемого диска,
b — номер стержня с которого снимается данный диск,
c — номер стержня на который надевается данный диск.
Например, строка 1 2 3 означает перемещение диска номер 1 со стержня
2 на стержень 3. В одной строке печатается одна команда.
Диски пронумерованы числами от 1 до n в порядке возрастания диаметров.
Программа должна вывести минимальный (по количеству произведенных операций) способ перекладывания пирамидки из данного числа дисков.
Указание: подумайте, как переложить пирамидку из одного диска? Из двух дисков? Из трех дисков? Из четырех дисков? Пусть мы научились перекладывать пирамидку из \(n\) дисков с произвольного стержня на любой другой, как переложить пирамидку из \(n+1\) диска, если можно пользоваться решением для \(n\) дисков.
Напишите функцию void move (int n, int x, int y),
которая печатает последовательнось перекладываний дисков для перемещения
пирамидки высоты n со стержня номер x
на стержень номер y.
| Ввод | Вывод |
|---|---|
2 |
1 1 2 |
Постановлением ЮНЕСКО оригинал Ханойской башни был подвергнут реставрации. В связи с этим во время пользования головоломкой нельзя было перекладывать кольца с первого стержня сразу на третий и наоборот.
Решите головоломку с учетом этих ограничений. Вам не нужно находить минимальное решение, но количество совершенных перемещений не должно быть больше 200000, при условии, что количество дисков не превосходит 10.
Тесты к этой задаче закрытые.
| Ввод | Вывод |
|---|---|
1 |
1 1 2 |
2 |
1 1 2 |
На дорогах Ханоя было введено одностороннее круговое движение, поэтому теперь диск со стержня 1 можно перекладывать только на стержень 2, со стержня 2 на 3, а со стержня 3 на 1.
Решите головоломку с учетом этих ограничений. Вам не нужно находить минимальное решение, но количество совершенных перемещений не должно быть больше 200000, при условии, что количество дисков не превосходит 10.
| Ввод | Вывод |
|---|---|
1 |
1 1 2 |
2 |
1 1 2 |
В Ханое несправедливо запретили класть самый маленький диск (номер 1) на средний колышек (номер 2).
Решите головоломку с учетом этих ограничений. Вам не нужно находить минимальное решение, но количество совершенных перемещений не должно быть больше 200000, при условии, что количество дисков не превосходит 10.
| Ввод | Вывод |
|---|---|
2 |
1 1 3 |
Первоначально все диски лежат на стержне номер 1. Переместите диски с нечетными номерами на стержень номер 2, а с четными номерами - на стержень номер 3.
Вам не нужно находить минимальное решение, но количество совершенных перемещений не должно быть больше 200000, при условии, что количество дисков не превосходит 10.
| Ввод | Вывод |
|---|---|
2 |
1 1 2 |
3 |
1 1 2 |
Как и в предыдущих задачах, дано три стержня, на первом из которых надето \(n\) дисков различного размера. Необходимо их переместить на стержень 3 по следующим правилам:
Самый маленький диск (номер 1) можно в любой момент переложить на любой стержень.
Перемещение диска номер 1 со стержня a на стержень b
будем обозначать 1 a b.
Можно поменять два диска, лежащих на вершине двух стержней, если размеры этих дисков
отличаются на 1. Например, если на вершине стержня с номером a лежит
диск размером 5, а на вершине стержня с номером b лежит диск размером
4, то эти диски можно поменять местами. Такой обмен двух дисков будем обозначать
0 a b (указываются номера стержней, верхние диски которых обмениваются местами).
Для данного числа дисков \(n\), не превосходящего 10, найдите решение головоломки. вам не нужно находить минимальное решение, но количество совершенных перемещений не должно быть больше 200000.
| Ввод | Вывод |
|---|---|
1 |
1 1 3 |
2 |
1 1 3 |
Дана полоска из клеток, пронумерованных от 1 до N слева направо. Разрешено снимать или ставить фишку на клетку с номером 1 или на клетку, следующую за самой левой из установленных фишек. Изначально полоска пуста. Нужно разместить фишки во всех клетках.
Программа получает на вход количество клеток в полоске \(N\) \((1\le N\le 10)\).
Программа должна вывести последовательность номеров клеток, с которыми совершается действие. Если фишка снимается, то номер клетки должен выводиться со знаком минус. Количество действий не должно превышать \(10^4\). Если существует несколько возможных решений задачи, то разрешается вывести любое.
Тесты к этой задаче закрытые.
| Ввод | Вывод |
|---|---|
3 |
1 2 -1 3 1 |
В небоскребе \(n\) этажей. Известно, что если уронить стеклянный шарик с этажа номер \(p\), и шарик разобьется, то если уронить шарик с этажа номер \(p+1\), то он тоже разобьется. Также известно, что при броске с последнего этажа шарик всегда разбивается.
Вы хотите определить минимальный номер этажа, при падении с которого шарик разбивается. Для проведения экспериментов у вас есть два шарика. Вы можете разбить их все, но в результате вы должны абсолютно точно определить этот номер.
Определите, какого числа бросков достаточно, чтобы заведомо решить эту задачу.
Программа получает на вход количество этажей в небоскребе \(n\) и выводит наименьшее число бросков, при котором можно всегда решить задачу.
Тесты к этой задаче закрытые.
| Ввод | Вывод |
|---|---|
4 |
2 |
20 |
6 |
Комментарий к первому примеру. Нужно бросить шарик со 2-го этажа. Если он разобьется, то бросим второй шарик с 1-го этажа, а если не разобьется - то бросим шарик с 3-го этажа.
Подсказки.
1. Как следует действовать, если шарик был бы только один?
2. Пусть шариков два и мы бросили один шарик с этажа номер \(k\). Как мы будем действовать
в зависимости от того, разобьется ли шарик или нет?
3. Пусть f(n) - это минимальное число бросков, за которое можно определить
искомый этаж, если бы в небоскребе было n этажей. Выразите f(n)
через значения f(a) для меньших значений a.